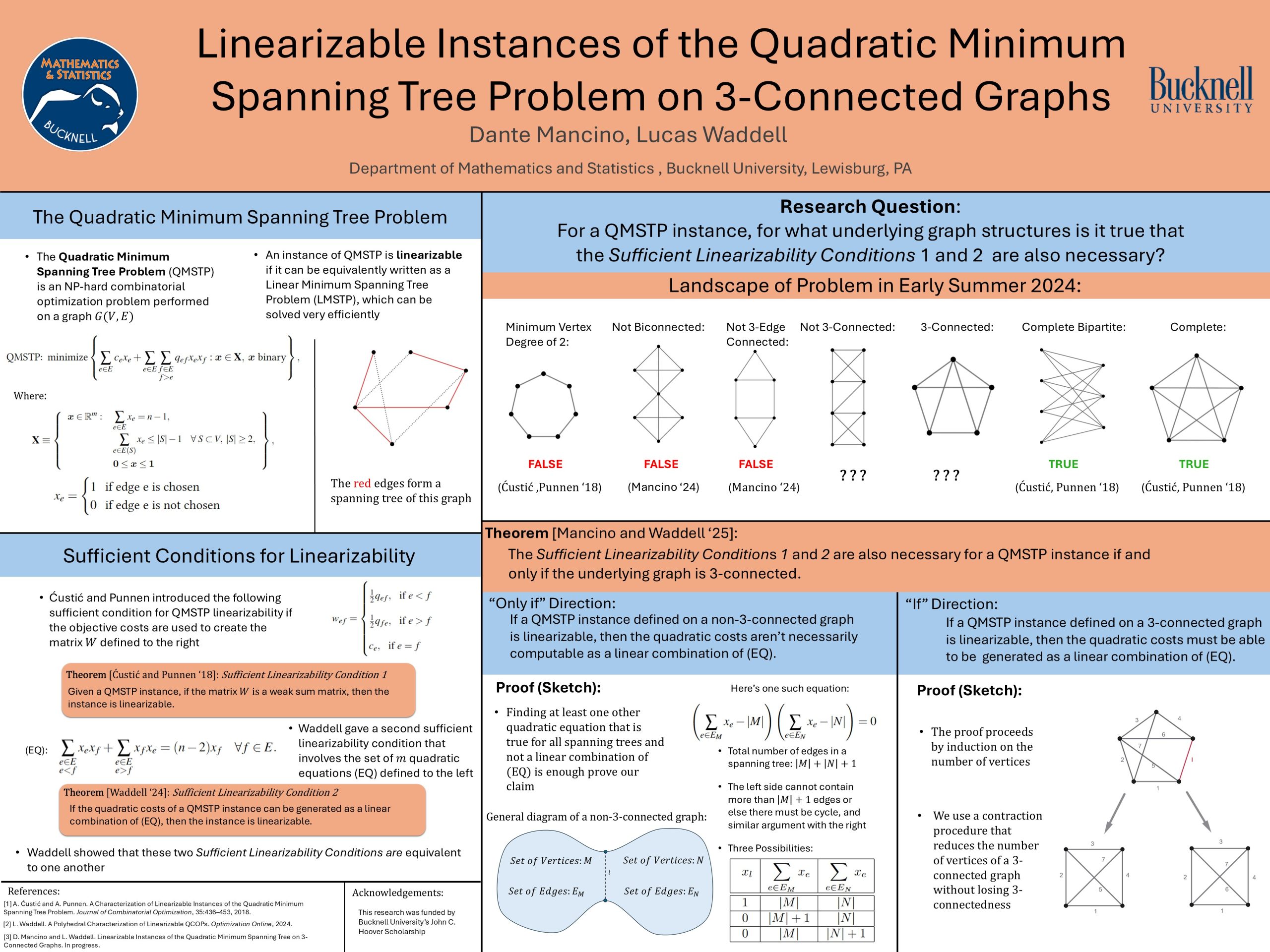
Linearizable Instances of the Quadratic Minimum Spanning Tree Problem on 3-Connected Graphs
Author:
Dante Mancino ’27Co-Authors:
Faculty Mentor(s):
Lucas Waddell, Mathematics and StatisticsFunding Source:
John C. Hoover ScholarshipAbstract
The quadratic minimum spanning tree problem (QMSTP) is graph-based combinatorial optimization problem that, in general, is notoriously difficult to solve. We study special easily-solvable instances of the QMSTP that are known as linearizable, meaning that the quadratic objective can be equivalently rewritten as linear in a manner that preserves the objective function value of each feasible solution. Previous work has shown that a sufficient condition for linearizability is that the (symmetric) matrix of cost coefficients is a weak sum matrix. This work also showed that this sufficient condition becomes necessary for linearizability when the underlying graph is a complete graph. In our work, we broaden this result by proving that this sufficient linearizability condition is necessary if and only if the QMSTP instance is defined on a 3-connected graph.